联通性相关/tarjan全家桶
1 对于无向图
1.1割点/割顶
对于一个无向图,如果把一个点删除后这个图的极大连通分量数增加了,那么这个点就是这个图的割点(又称割顶)。
tarjan算法:
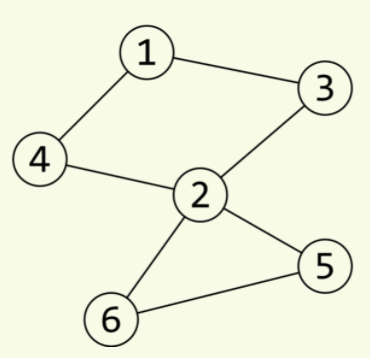
发现这张图只有一个割点 就是2;
首先我们在这上面进行一次dfs
打上时间戳
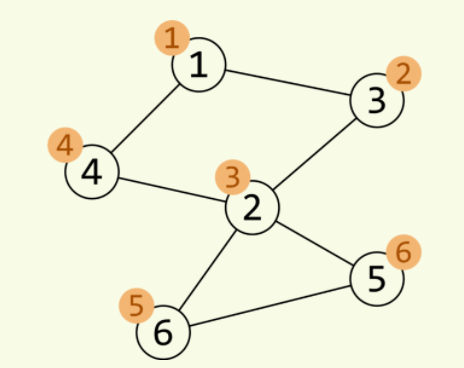
使用另一个数组low 存储不经其父能到达的最小时间戳
也就是除dfs遍历路外其他路所能到达的dfs遍历路上最前节点
判断某节点是否是割点的依据是对于某节点u 如果至少存在一个其子节点v使得
$low_v>=num_u$ 即不存在另一条路回到祖先 则u为割点
另外 若整颗dfs树的根由两颗及以上的子树 则其为割点
1.2 桥/割边
对于一个无向图,如果删掉一条边后图中的连通分量数增加了,则称这条边为桥或者割边。严谨来说,就是:假设有连通图 G={V,E},e 是其中一条边(即 e∈E),如果 G−e 是不连通的,则边 e是图 G 的一条割边(桥)。
例如
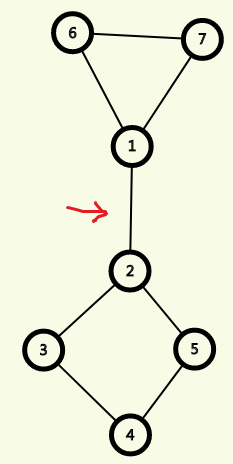
tarjan算法:
与割点几乎相同 但注意到 若$low_v=num_u$ 即其子节点可以通过另一条边回到该节点 则不认为其为割边 同理不必考虑根的问题
1.3 边双联通分量
在一张连通的无向图中,对于两个点 u 和 v,如果无论删去哪条边(只能删去一条)都不能使它们不连通,我们就说 u 和 v 边双连通。
某分量中若所有点都边双联通 则称该分量为边双联通分量
首先使用tarjan求出所有割边
删除所有桥后所得分量即为边双联通分量
1.4 点双联通分量
在一张连通的无向图中,对于两个点 u 和 v,如果无论删去哪个点(只能删去一个,且不能删 u 和 v 自己)都不能使它们不连通,我们就说 uu 和 vv 点双连通。
分量与上例相似
但点双联通不具传递性 如图中 A,B B,C A,C
当某节点第一次被访问是将此节点入栈
若达到判定割点条件后将栈一直弹出至子节点弹出
然后所有弹出节点与父节点构成一个点双联通分量
缩点
我们将每个割点与每个点双建点连边即可
2 对于无向图
与上文所述无异的维护两个数组dfn和low 发现对于某节点若dfn与low值相同 则栈中其后节点构成一个强联通
