GarsiaWachs
算法流程
1.找到满足 $q_{k-1} \lt q_{k+1}q$的最小下标 kk
2.找到满足$q_{j-1} \gt q_{k-1} + q_kq$的最大 $j \lt kj<k$
3.从列表中清除$q_{k-1}, q_kq$
4.在$q_{j-1}q$ 之后插入 $q_{k-1} + q_kq$
5.$q_{-1}$和$q_{n+1}$n+1可以用 \infty∞ 处理
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| #include<bits/stdc++.h>
using namespace std;
#define INF 0x7fffffff
vector<int> a;
int n,t,ans=0,k,j;
int main()
{
cin>>n;
a.push_back(INF);
for(int i=1;i<=n;i++)
cin>>t,a.push_back(t);
a.push_back(INF);
while(n-->1)
{
for(k=1;k<=n;k++)
if(a[k-1]<a[k+1]) break;
int s=a[k-1]+a[k];
for(j=k-1;j>=0;j--)
if(a[j]>a[k-1]+a[k]) break;
a.erase(a.begin()+k-1);
a.erase(a.begin()+k-1);
a.insert(a.begin()+j+1,s);
ans+=s;
}
cout<<ans;
return 0;
}
|
证明
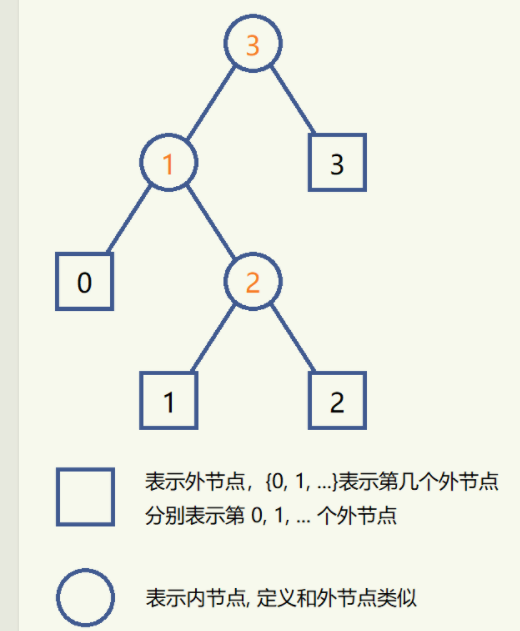
本算法基于最优二叉树提出
二叉树中预期比较次数