首先 应该清楚三点

1 endpos数组只是我们为了说明后缀自动机性质的辅助数组 我们在建造自动机时并不需要知道endpos是啥 只需要明确建出的自动机满足endpos即可

2 利用parent树说明后缀自动机只是为了证明它的某些性质 后缀自动机和parent树或许有半毛钱关系

3 后缀自动机的后缀trie合并论不只是在介绍它有什么用 如果想真的理解它应该真的用trie合并的角度去理解

那么我们正式开始介绍

问题的引入

如果 我们把一个字符的所有的后缀插入一颗字典树

发现从根开始的每一条路径都对应一个子串

联想到这样可以干很多事

但是这样最差空间复杂度很大 我们应该想办法去压缩它

于是引出SAM

定义

1 存在一个源点和若干终止点 边(转移)的定义与trie相仿

从源点到任意一个节点的任意路径应当是一个字符串

2 从源点到任意节点的任意路径形成的字符串均为原串字串从源点到任意节点的路径不能形成的字符串不是原串子串

3 从源点到任意终止节点的路径形成的字符串为原串后缀

4 从源点出发任意两条不同的路径形成的字符串最小

5 即在满足上述定义的所有DAG中我们要最小的那个

基本思想

1 endpos

我们定义endpos(p)为原串中p出现的所有位置所构成的集合

例如对于串$\text{abcab}$ endpos(ab)={2,5}

引理1

如果两个串的endpos相同 那么其中一个字串必定为另一个的后缀

正确性显然

引理2

对于任二字串t,p ($len_t<=len_p$) 要么endpos(p)被包含于endpos(t),要么endpos(t)与endpos(p)不重 且仅当t不是p的后缀

与引理1同理

引理3

对于endpos相同的字串 我们将他们归为一个endpos等价类 对于任意endpos等价类 将包含在其中的所有字串依长度从大到小排序 则字串长度连续且均为上个的后缀

发现若endpos相同 则长度小的必定为长度大的的子串

若某两个字串存在于一个等价类且他们长度相差2 则他们长度隔一个夹中间的那个子串必定的也存在于这个等价类 可以感性理解下 前后两个夹着它的都在这些位置出现 则它必定不能在其他位置出现

引理4

endpos等价类数量级为O(n)

这个命题的结论与SAM的复杂度相关 且证明是构造的基础

我们详细的证明一下

对于一个等价类 其中存在一个最长的字串P 在P的第一个字符前添加任意字符 得到的字符串必定不属于此类 并且若加入的字符不同 则二等价类必完全不相交根据加入的字符的不同 我们将原本的等价类分割成不同的几个等价类

SAM构造原理

我们发现如果两个节点代表的字串的endpos属于同一个等价类 那么我们就可以把他们合并 于是如果发现两个节点的endpos不属于同一个等价类 我们就不能把他们合并 于是 我们就可以按照endpos等价类来区分两个节点能否合并 若加入一个点 我们倒序的去检查它和它之前的各个等价类是否存在转移边存在就连上

SAM构造过程

sam使用增量构造 即每次加入字符串末尾的一个新字符 从原先的SAM变成新的SAM

考虑若在原串的后缀字典树上增量会发生什么:

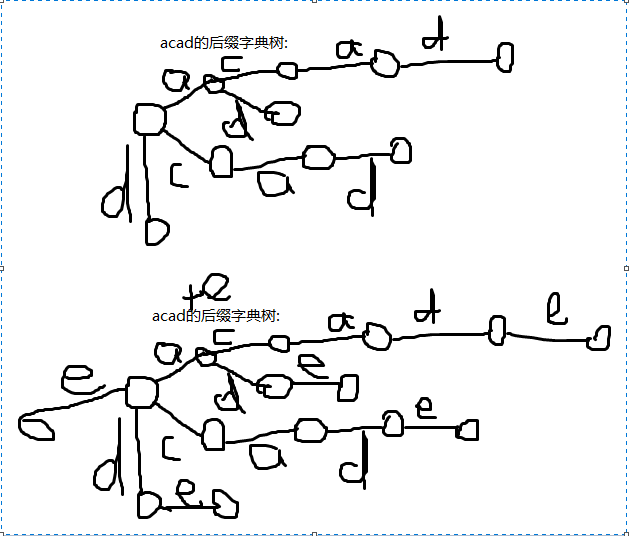
就是在所有节点后面都加了一个e

那么考虑增量后维护SAM的性质

先展示一下我们用算法构造的SAM的构造: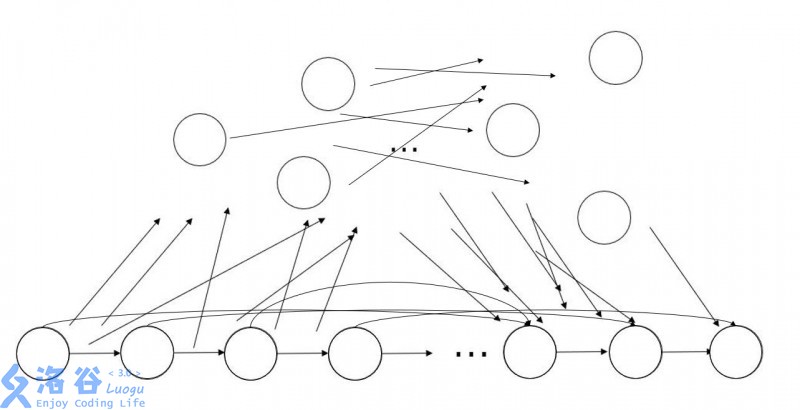

下面一排整齐的节点就是原串各个前缀所代表的节点

加入一个字符c 整个串必定是一个新的等价类 于是我们

新建一个下面一排整齐的节点连到上一个去

发现依上面trie的讨论我们应该让上个节点的后缀都连出一条c边 但是有些后缀归结为了同一个等价类 我们就跳parent trie上的边(fail指针)

case1

如果跳到的节点本身没有c出边 就说明它代表的字串后面从来没有接上过c (想一想 为什么(从trie的角度)) 那么它所代表的等价类中的所有字串再加上一个字符c必定还都属于同一个等价类 且只在最后一个点(c点)出现 于是我们就把它囸掉连到这个新建的节点即可

case2

如果跳到的节点本身就有c出边 并且它出边到了的点的等价类中的最长串的长度等于它这个点的等价类中的最长串的长度+1 (这也就说明出边到了的点的等价类中只有一个字串 而如果我们再加入C 那么等价类仍是那个等价类 (并且出现位置加了N 因为它必是原串后缀(想一想为什么)) 忽略即可)这与我们在trie上的处理相同

case3

问题来了 如果 他们的长度和上述不符怎么办呢 我们发现longest(q)必定不是新串的后缀 若是 则去掉字符c后的字符串必定是原串的后缀 他会先被跳到 因此 q的等价类中存在一些字串出现在末尾 其长度不大与len(p)+1 另一些不出现在末尾 其长度大于n 这样加入c后这个等价类就不是一个等价类了 它被分裂了 我们应该分开它